Electricity is a uniquely convenient way of using an energy source. It gives us instant energy at the flick of a switch; it allows us to use energy in densely populated areas while burning fossil fuels remotely; and recently it has allowed us to capture energy from renewable sources such as the wind and the sun.
However, this convenience comes at a price. Electricity is not a primary energy source. This means that there have been losses in the system before it reaches the point of use. There are further losses in all electrical appliances. Reducing all these losses can lead to great savings to the economy and the environment.
In this e-source we’ll look at how electricity is generated, distributed and used and copper’s role in making these activities more efficient.
There are 4 Copper and Electricity units as below.
| Introduction | Efficient Motors | Generation | Transformers and the Grid |
|
|
|
|

Electricity provides us with energy at the flick of a switch.
Electrical Efficiency
Generating and distributing electricity
Note: this section reflects the situation in EU & UK at the turn of this century. Meanwhile, the electricity system is rapidly decarbonising, to the extent that it is currently dominated by low-carbon power generation. The paragraphs below no longer reflect the current situation and need updating.
Although electricity is very convenient, we aren’t always conscious of the waste associated with its use. Over 50% of EU electricity comes from fossil fuels, mainly coal, which accounts for about 30% of overall electricity generation in the EU. Burning these fuels has an environmental impact releasing carbon dioxide (a greenhouse gas) and sulfur compounds into the atmosphere. Fossil fuels are finite resources and any waste in the system means that we are consuming them more quickly than our great grandchildren would like.

Whether electricity is generated from fossil fuels or renewable sources such as solar and wind power, efficiency of generation, distribution and use is critical.
Table 1 below shows the energy losses and the environmental impact of our use of electricity. The unit tonne of oil equivalent (TOE) is a useful way of comparing energy use–relating it to fuels. 1 TOE equals 11,634 kilowatt–hours. In the UK, 1 kWh produces 0.51 kg of carbon dioxide; this takes into account the different ways in which electricity is generated (15% is generated without producing any carbon dioxide).
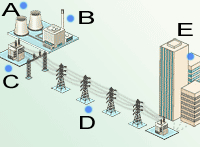
See Table 1 for losses and wastage at each stage of generation, distribution and use of electricity.
Table 1: Losses in the UK electricity system.
| Component | Description | % Efficiency |
Annual wastage in UK Billion kWh |
Million TOE | Million tonnes CO2 |
| A. Thermodynamic restraints | A traditional fossil fuels power station burns the fuel to boil water into steam. The steam drives turbines to turn the generator. The steam is then cooled to condense it back into water. There is no way of avoiding the need of this system to heat up the surroundings. It will always be inefficient. | 38 | 800 | 68.8 | 408 |
| B. Generators | In coal, oil and nuclear power stations, the generators are turned by the steam turbines. From this movement, they generate a voltage which can drive a current into the transmission system. | 95 | 39 | 3.4 | 19.9 |
| C. Generator transformers | Transformers are used to step the voltage up at the power station and to step it down close to the end-user. The transformers at the generator end are usually state of the art and highly efficient. | 99.5 | 2.2 | 0.2 | 1.1 |
| D. Distribution system | This includes the step down transformers and the cables, which carry the electric current from the power station to the end-user. All the wires have electrical resistance and therefore get hot, wasting some of the energy as low grade heat in the atmosphere. | 92 | 35 | 3.0 | 17.9 |
| E. End use e.g. motor | We use electricity for heating, cooking, driving things (motors) and electronic appliances. All of these have inefficiencies – usually wasting energy as low grade heat. | 88 | 49 | 4.2 | 24.9 |
| Total (electrical total) | The total efficiency is low. Notice that, for similar percentage losses, the actual losses get smaller later on in the system. This is because there is less energy being transmitted at the later stages. | 28 (74) |
930 (340) |
79.9 (28.9) |
474 (171) |
Using electricity
The distribution system loses (as heat) about 8% of the energy that is supplied to it – i.e. it is 92% efficient. The generation system is less efficient. A conventional power station is about 35% efficient – although modern combined heat and power (CHP) plants can have efficiencies approaching 60%. Most of the losses in the power station are inherent in the thermodynamic processes with the generators being about 92% efficient.
So, by the time we use the electricity, it only represents about 33% of the original energy content of the fuel. There is then a further loss in the appliance that we use. For a standard motor, this would be about 12%, making the whole system about 28% efficient.
If we can improve efficiency, then this reduces the cost, the environmental impact and the rate at which we are using up precious fossil fuel reserves. Efficiency can be thought of as the third fuel – an alternative to alternative energy sources.
Comparing losses
The overall efficiency for electricity generation and use may seem very low, but it has to be compared with uses of other fuels. In a car, about 15% of the primary energy of the fuel is available at the wheels – not including the losses involved in transporting petrol from refinery to the point of use. A domestic gas boiler has a thermal efficiency of about 70% – again neglecting the energy required to pump gas around the country – but much of the heat output merely heats up building voids and structure so the useful output is much lower.
Not only must new energy sources, particularly renewable ones, be developed, but we must improve the efficiency of use of existing resources. Copper has a vital role to play in improving the efficiency of electrical appliances and electricity distribution.
Reducing losses
Electrical engineers have to consider energy efficiency when they are designing new systems. When electric currents flow and when magnetic fields change, there are energy losses – things get hot when we don’t want them to. This waste costs money, and results in increased environmental damage.
60% of all the copper produced worldwide is used in electrical applications. It is used in electric motors and generators, transformers, wires and cables, printed circuit boards and microchips.
Copper Cables
Copper and energy efficiency
Copper is a very good electrical conductor. This means that the resistance of a length of copper cable is relatively low. An aluminium cable would have nearly twice the resistance of a copper cable with the same dimensions. Therefore the energy losses in the aluminium cable will be higher than in the copper cable. The copper cable is more energy efficient.
To make an aluminium cable with the same energy losses as a copper cable, we have to make it fatter. The larger cross sectional area reduces its resistance and brings the energy losses down to the same as a narrower copper cable.

Cables made from copper and aluminium. The aluminium cable has nearly twice the area to give it the same resistance as the copper cable. You can see the strands of conductor and the armour.
The two cables in the photograph have similar current-carrying capacity. They are each designed to be able to carry up to 500 A without the conductor going above 90°C; they will have to carry this current when demand is high but should not be used for larger current.
The copper cable (on the left) is thinner than the aluminium one, because copper is a better conductor. Its cross sectional area is 300 mm2 as opposed to 500 mm2 for the aluminium.
There are four groups of wires within the cable and the groups are insulated with cross-linked high-density polyethene (XLPE). The whole is reinforced with steel wire armour.
What are the advantages of copper?
The copper cable has several advantages over the aluminium one. Because it is thinner, it can fit into smaller duct spaces. It can be bent around tighter corners. Also, copper can be easily jointed.
Copper is three times as dense as aluminium. An aluminium cable is half the weight of a copper one with the same rating, so aluminium cables (reinforced with steel) are often preferred for hanging between overhead pylons.
For a complete comparison of energy-efficiency, we should also take into account the energy used in mining, refining and transporting these metals.
What is the safe operating current?
The current rating of a cable is the current it can carry safely without overheating. The main issue is that the temperature of the conductor should not rise above 90°C because this will cause the insulation to degrade and eventually break down. A cable should always be protected by a protective device – a fuse or circuit breaker – that corresponds to its current rating. The transmission cables in the above picture will be in series with a 500 A protective device which will break the circuit before the current is high enough to cause the cables to overheat.
The operating current of a cable is determined by how hot the cable gets. This is affected by a number of variables:
- the resistance of the cable – a higher resistance cable will get hotter at a given current
- the insulation on the cable – this will tend to keep it warm
- the environment of the cable – if it is in a duct (especially with no airflow) it will tend to get hotter.
Copper plays a part in improving the current rating of cables because it is such a good conductor.
Electrons and Current
How current flows
Copper is a good conductor because, like other metals, it contains free electrons. Free electrons are also known as conduction electrons. Each copper atom provides a single free electron, so there are as many free electrons as atoms. (See Figure 1).
Free electron concentration in copper, n = 8.5 × 1028 per m3
When a voltage is connected across a piece of copper, it pushes the free electrons so that they flow through the metal – that’s an electric current (see Figure 2).
About current
The electrons start to flow as soon as the switch is closed. The message to get them moving is instantaneous (in fact it travels close to the speed of light). However, the electrons themselves travel much more slowly. So how does the current come on everywhere as soon as the switch is closed?
It is because the free electrons are already spread through the wire. As soon as the switch is closed, there is a force on all the electrons, which gets them moving. It’s a bit like a bicycle chain. As soon as you start pedalling, the back wheel starts to turn. The force on the back wheel is instantaneous even though the individual links are travelling at a visible speed. But because the links are already spread around the chain ‘circuit’ they all start to move at the same time.

Figure 1: A copper wire is made of a lattice of copper ions. There are free electrons that move through this lattice like a gas. Note the copper ions vibrate.
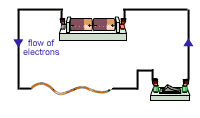

Figure 2: Operating the switch in the circuit (above left) causes electrons to flow from left to right, in the opposite direction of the current.
Electron velocities
Even when no current flows through a piece of copper, the free electrons are moving rapidly about (see Figure 1). Their speed is about 106 m s-1; that’s 3000 times the speed of sound in air! However, since they are moving at random, there is no net flow of electrons in any particular direction and so there is no current.
When a voltage is applied, the electrons gain an additional velocity, so that there is a net flow along the wire. This extra velocity is called their drift velocity.
Here’s a way to picture this: think of a swarm of bees. They are all milling around the hive. Each bee is moving, but the swarm stays still. Now one sets off and the rest follow. The swarm is still a milling mass, but overall it moves away from the hive. The free electrons in a metal are like the bees; it takes a voltage to make the mass of electrons move through the wire.
Current direction
Electrons are negatively charged, they flow from negative to positive in a circuit. Conventional current flows the other way – from positive to negative.
Drift Velocity
Drift velocity and current
How fast must free electrons move in a wire to produce a decent current?
‘Current’ means the rate at which electric charge flows past a point in a circuit. Imagine standing at point X with a stopwatch and timing the charge flowing past in a cylinder with volume V (we have to imagine that all the electrons move at the same speed, v). We’ll watch what happens to a specific electron.
Suppose you start your watch and let it run for a time, t. The electron will have travelled a distance L. In fact, in time t, all of the electrons in a cylinder of length L have flowed past you.
So what current has flowed? We need to work out how much charge has passed.
We start by thinking of the volume of the cylinder.
Volume of cylinder = A × L where A is the cross-sectional area of the wire
If concentration of electrons in the metal is n per cubic metre then:
Number of electrons in cylinder = n × A × L
If each electron carries charge Q then:
Charge carried by electrons in cylinder = n × A × L × Q
But the length of the cylinder is v * t, where v is the drift velocity and t is the time we used, so:
Charge carried by electrons in cylinder = n × A × v × t × Q
This is the amount of charge which passes point A in time t. To find the current which this represents, we need to find the rate at which the charge has flowed. So we divide by the time t.
Current = charge / time = n × A × v × t × Q / t = n A v Q
So the electric current I flowing in a wire is given by
I = n A v Q
where n is the number of electrons per cubic metre
A is the cross sectional area of the wire
v is the drift velocity of the electrons
Q is the charge of an electron.
Resistivity and charge density
A material with a lot of free electrons (a high value of n) can carry a current more easily than one with a smaller charge density. To carry a given current, the electrons don’t have to move very fast because there are so many of them to carry the charge. This means that they rarely collide with atoms or impurities in the metal, and so it is a good conductor.
Semiconductors are materials with few free electrons – perhaps one-millionth of copper’s concentration. So free electrons in semiconductors have to have much higher drift velocities to carry the same current. Their speed has to make up for the smaller amount of charge that is moving. Therefore they collide with atoms much more often. The resistivity of a semiconductor is typically one million times that of copper.
How fast do electrons drift?
We can get an idea of how fast the drift velocity is by taking some typical values of current and wire dimensions. Let’s think of a current of 5 A that is flowing in a copper wire with a cross section of 0.5 mm2 (= 0.5 * 10-6 m2):
For copper, n = 8.5 × 1028 per m3
The charge on an electron, Q = 1.6 × 10-19 C, so:
I = n A v Q
5 = 8.5 × 1028 × 0.5 × 10-6 × v × 1.6 × 10-19
5 = 27 200 v
v = 7.35 × 10-4 m s-1
So, for this current, the drift velocity of electrons is about a tenth of a millimetre per second: pretty slow!
Resistance and Heating
Understanding resistance
| How the resistance varies | Explanation |
| Resistance decreases as copper (or any other metal) is cooled. | Its atoms vibrate less, and so they impede the flow of electrons less. |
| Pure copper has less resistance than copper containing impurities. | Impurity atoms are a different size to copper atoms, so they get in the way of moving electrons. |
Transferring energy
When we apply a voltage to a wire, the conduction electrons drift through the wire, forming a current. Now let’s concentrate on a few electrons. Each time an electron collides with an ion, it loses energy. This energy is transferred to the ion (which vibrates more); eventually the energy from billions of collisions is shared amongst all the atoms, and the material gets hot.
This is often called joule heating, and it is something electrical engineers try to reduce – unless they are designing a heater!
Once the ions are vibrating, they hinder the flow of the electrons. This is because the electrons will be scattered off the vibrating ions. As the wire gets hotter, the ions vibrate more vigorously. This makes it more difficult for electrons to pass along the wire. Hence the resistance increases.
How quickly is energy transferred?
The rate at which energy is transferred is power. Power is measured in watts and one watt is equivalent to one joule per second. The power dissipated in a piece of wire will be related to the voltage across the ends of the wire and the current flowing through it.
In fact:
electrical power = voltage × current
P = V I
Quick check using units
It often helps to check an equation works when you put the units into it. So, in this case, if we put the units for voltage and current into the right hand side of the equation, we should get the units of power.
The voltage is the potential difference i.e. the difference in potential energy per unit charge. It tells us how much energy is transferred per coulomb of charge that flows. The bigger the voltage, the more energy each coulomb will transfer. So power will increase with voltage.
A good way to remember this is through the more basic units of the volt. One volt is equivalent to one joule per coulomb.
[voltage] = V = J/C
[coulomb is the unit of charge]
The current is how quickly charge is flowing. The bigger the current, the more charge flows through the wire in a given time and the more energy it can transfer. So the bigger the current, the bigger the power.
One amp is equivalent to one coulomb per second
[current] = A = C/s
We can put the units into the equation for power:
[power] = [voltage] x [current] = J/C × C/s = J/s = W
This is the unit for power. So the equation works!
Another equation for power
In transmission systems, we often know the current being drawn through a cable and the resistance of the cable. Although we may know the voltage of the source, we may not know the voltage drop across the wire. In this case, we can use an alternative version of the equation for power:
P = I2 R
[You can get this equation by substituting V = I R into the first equation for power.]
Energy efficient Cables
Choosing a cable
Industrial premises such as factories, office blocks and shopping centres are supplied with electricity through thick cables. These cables may get hot as currents of hundreds of amps are made to flow through them.
How is the best cable chosen? We need to consider:
- installation costs.
- running costs.
In summary, the thick cable costs more to install but is less expensive to run.
Installation: Most of the cost of installing a cable goes on accessories, digging trenches, installing cable trays, and labour. The cost of cable may be 10 to 15% of the installation cost. So even doubling the cost of the cable has only a small effect on total cost. Thicker cables also allow for increased demand in the future.
Running costs: Thicker cables have a lower resistance. This means that they are less wasteful.
Imagine a factory that needs to draw 200 amps from the National Grid to run its machines. This current will heat up the cables that supply the factory. The amount of power wasted in these cables by joule heating is given by the expression:
P = I2 R
To keep this power as small as possible, the resistance of the cable should be as small as possible, so thicker is better. This also allows for an increase in demand in the future.
Also, a thinner cable gets hotter. So fans or air-conditioning may be needed to remove the heat. These add to the running costs.
Did you know?
Copper is the best non-precious conductor of heat and electricity. Only silver is a marginally better conductor, and as a precious metal that cannot be used widely in conductive applications.
Questions
1. At 99.5% efficient, transformers are the most efficient part of the distribution system. However, they still waste the equivalent of 100,000 tonnes of oil per year. Imagine we improved their efficiency to 99.7%. How much oil equivalent would this save?
2. The voltage drop across 1 km of copper cable is 30 V at 500 A. Calculate the resistance.
3. In a piece of metal, when no current is flowing, the conduction electrons are moving around randomly. What is their average velocity?
4. The conventional direction of an electric current is the opposite of the direction of motion of the electrons that carry it. Why do you think this is so?
5. Calculate the drift velocity of electrons in a copper wire of cross-sectional area 1 mm2 when a current of 2.5 A flows through it.
>> Continue to Copper and Electricity: Efficient Motors (16-18)
 |
 |
Comments
0 comments
Please sign in to leave a comment.